Mentioned Monte Carlo (also translated as "Monte Carlo"), people can not help but think of Monaco's casino. Is there a necessary connection between the two? The answer is: Exactly!

Everyone thinks about what gambling is about. The first thing that comes to mind is randomness and probability. Yes, the Monte Carlo method is related to probability theory and mathematical statistics.
  MCM proposes:
The Monte Carlo Method MCM was first proposed by SM Ulam and J. von Neumann (the father of computers) in the United States during the 1940s when the United States developed the "Manhattan Project" program for atomic bombs in the Second World War. The mathematician von Neumann named this method with the famous casino of the world, Monte Carlo of Monaco, and cast a mystery on it. Before that, the Monte Carlo method already existed. In 1777, the French mathematician Georges Louis Leclere de Buffon proposed using the needle experiment to determine the pi. This is considered to be the origin of the Monte Carlo method.

The traditional empirical method can't get close to the real physical process, so it is difficult to get satisfactory results. Because the Monte Carlo method MCM can realistically simulate the actual physical process, solving the problem is very consistent with the actual situation, and a very satisfactory result can be obtained. This is also a calculation method based on theoretical methods of probability theory and mathematical statistics. It is a method that uses random numbers (or, more commonly, pseudo-random numbers) to solve many computational problems. The problems solved are connected with the same fixed probability model, and statistical simulation or sampling is performed with the computer to obtain the approximate solution of the problem. To symbolically show the probability and statistical characteristics of this method, it is borrowed from the name of Casino-Monte Carlo. The naming reflects not only part of the content of the method, but also facilitates memory, so it is generally accepted by people.
BTW: The word Monte Carlo originated from Italian to honor Prince Charles III of Monaco. Although Monte Carlo is a casino, it is small and is estimated to be almost as big as a street in Beijing.

MCM Overview:
The Monte Carlo Method (MCM), also called random sampling or statistical simulation method, was developed in the mid 1940s due to the development of science and technology and the invention of electronic computers. A very important type of numerical method for guidance. Refers to the use of random numbers (or pseudo-random numbers) to solve many computational problems. Corresponding to it is a deterministic algorithm. The Monte Carlo method is widely used in financial engineering, macroeconomics, computational physics (such as particle transport calculations, quantum thermodynamic calculations, aerodynamic calculations), and machine learning in artificial intelligence .
The basic idea of ​​MCM:
When the problem being solved is the probability of some kind of random event, or the expected value of some random variable, the probability of this kind of random event is estimated by the frequency of this kind of event through an “experimental†method, or this random Some of the numerical characteristics of the variable are treated as solutions to the problem.
The dimension (number of variables) of a class of problems may be as high as hundreds or even thousands, and the difficulty of problem solving increases exponentially with the increase of dimensions. This is the so-called Curse of Dimensionality. Even with the fastest computers, the traditional numerical methods are difficult to deal with, but the computational complexity of the Monte Carlo method MCM is no longer dependent on the dimension, and MCM can be used to deal with the disaster of dimensions. To improve the efficiency of the method, scientists have proposed many so-called "variance reduction" techniques.
The other form is similar to the Monte Carlo method MCM, but the method with different theoretical foundations—Quasi-Monte Carlo method—has developed rapidly in recent years. The “Hua-Wang†method proposed by Chinese mathematician Hua Luogeng and Wang Yuan is one example. The basic idea of ​​this method is to replace the random number sequence in the Monte Carlo method MCM with deterministic Low Discrepancy Sequences. This method solves certain problems faster than the Monte Carlo method MCM. Hundreds of times, the calculation accuracy has also greatly improved.
The basic principle of MCM
According to the definition of probability, the probability of an event can be estimated by the frequency of the event in a large number of experiments. When the sample size is large enough, the frequency of the event can be considered as its probability. Therefore, a large number of random variables are firstly applied to the random variables that affect their reliability, and then the sampled values ​​are grouped into a functional formula to determine whether the structure fails. Finally, the structural failure probability is obtained. MCM is based on this idea for analysis.
There are statistically independent random variables Xi (i=1, 2, 3,..., K) whose corresponding probability density functions are fx1, fx2,..., Fxk, and the functional formula is Z=g(x1, x2, ..., xk).
Firstly, according to the corresponding distribution of random variables, N sets of random numbers x1, x2,..., xk are generated, and the functional function value Zi=g(x1,x2,...,xk) (i=1,2,...,N) is calculated. If there is a functional function value corresponding to the L-group of random numbers Zi ≤ 0, then when N → ∞, according to Bernoulli's theorem of large numbers and the characteristics of normal random variables, there are structural failure probabilities and reliability indices.
From the perspective of MCM, we can see that MCM can avoid the mathematical difficulties in structural reliability analysis. Whether the state function is non-linear or if the random variable is not normal, a more accurate failure probability can be obtained as long as the number of simulations is sufficient. And reliability indicators. Especially when the coefficient of variation is large, compared with the reliability index calculated by the JC method, the result is more accurate, and because the idea is simple and easy to program.
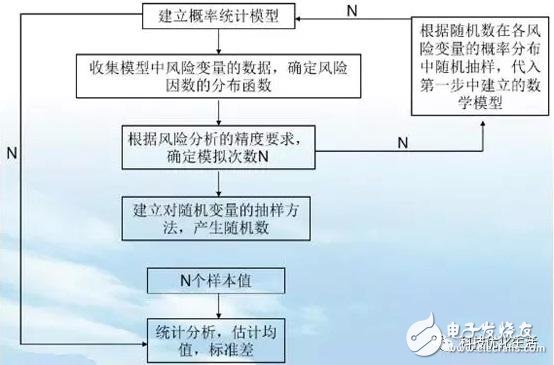
MCM main steps:
The Monte Carlo method work process can be attributed to three main steps:
1) Construct or describe probability processes
For a problem that itself has a random nature, it is mainly to correctly describe and simulate this probability process. For a deterministic problem that is not originally of a random nature, an artificial probability process must be constructed beforehand. Some of its parameters are exactly the solution to the required problem. . That is to say, problems that do not have a random nature are turned into random problems. To make an inappropriate comparison, there are difficulties in work and we must meet difficulties; if we have no difficulties, we must also create difficulties, and then meet difficulties. ^_^
2) Achieve sampling from a known probability distribution
After constructing the probabilistic model, since various probabilistic models can be regarded as consisting of various probability distributions, generating a random variable (or random vector) with a known probability distribution becomes a Monte Carlo method simulation. The basic means of experimentation is also the reason why the Monte Carlo method is called random sampling. Random numbers are random variables with a probability distribution. Random numbers are the basic tools for implementing Monte Carlo simulations. A sequence of random numbers is a simple subsample of a population that has this distribution, that is, a sequence of independent random variables that has this distribution. The problem of generating random numbers is the sampling problem from this distribution. On a computer, random numbers can be generated by physical methods, but they are expensive, cannot be repeated, and are inconvenient to use. Another method is to use mathematical recursive formulas. The sequence thus generated is different from the true random number sequence and is called a pseudo-random number (or pseudo-random number sequence). However, after various statistical tests have shown that pseudo-random numbers (or pseudo-random number sequences) have similar properties to true random numbers (or random number sequences), they can be used as true random numbers.
3) Establishing various estimates
After constructing the probability model and sampling from it, that is, after implementing the simulation experiment, we must determine a random variable as a solution to the required problem, and call it an unbiased estimate. The establishment of various estimators is equivalent to examining and registering the results of simulation experiments and obtaining solutions to these problems.
Usually, the Monte Carlo method solves various practical problems by constructing a random number that meets certain rules. The Monte Carlo method is an effective way to find numerical solutions for problems that are too complex to be solved analytically or have no analytical solution at all.

MCM work process:
The application of the Monte Carlo method when solving practical problems mainly has two parts:
1. When a Monte Carlo method is used to simulate a process, it is necessary to generate a random variable with a certain probability distribution.
2. Statistical methods are used to estimate the numerical characteristics of the model to obtain a numerical solution to the actual problem.
In theory, the Monte Carlo method requires a lot of experimentation. However, the solution is an approximate solution. The larger the number of simulation samples and the more experiments, the more accurate the results obtained. However, the increase in the number of samples will bring about a substantial increase in the amount of calculations.
MCM estimates pi:
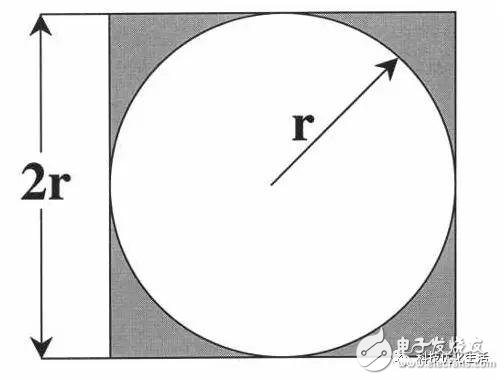
The Monte Carlo method can be used to, for example, make a circle with radius r in a square with side length 2r, the area of ​​the square is equal to 2r & TImes; 2r = 4r^2, the area of ​​the circle is equal to π & TImes; r & TImes; r = πr ^2, it can be concluded that the ratio of the area of ​​the square to the area of ​​the circle is 4:π. Suppose that darts are randomly thrown on a square target. If the hit points are uniformly distributed on the target, ie, the coordinates of a certain point are scattered in the square, then the number of points N falling within the square and falling within the circle are The ratio of the number of points K is close to the ratio of the area of ​​the square to the area of ​​the circle, that is, N:K ≈ 4:π, therefore, π ≈ 4K/N . Using this method to find the pi, a large number of uniformly distributed random numbers is required to obtain more accurate values.

MCM evaluates the Go board:
We all know Google's DeepMind Go program AlphaGo and it exceeds the powerful computing power of humans. In fact, the Monte Carlo method idea is also used in the evaluation of the Go board. Each Go board has an “optimal valueâ€, which corresponds to the final result of the Go board surface obtained by both players using perfect moves. For Go, it has been proved that the calculation of this "optimal value" takes at least an exponential increase with the number of steps from the disk to the final disk. For example, with an average of 200 steps, the number of possible disks per step increases by an average of 200 times. Theoretically, it is impossible to obtain the "optimal value", so people think of using the Monte Carlo method to sample the entire likelihood space, and then approach this "optimal value" by means of statistical evaluation. This is a dynamic assessment method called Monte Carlo Search proposed in 2006.
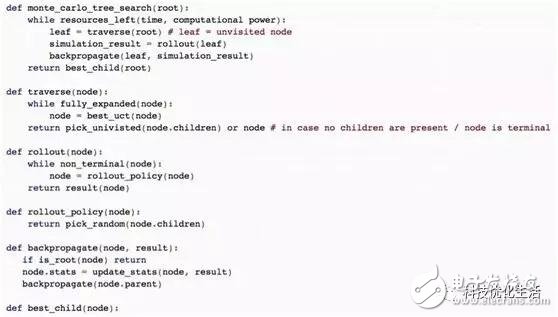
Although the existing Monte Carlo search can ensure that the results of a large number of samples are sufficient to converge to the “optimal value†on the disk, the number of samples required to achieve “sufficient convergence†still increases exponentially with the scale of the entire possible space. However, in the practice of the Go chess game system, Monte Carlo search actually shows far more power than the traditional method in the case of limited game time. In recent years, people have added more expert knowledge related to Go in the selection strategy, which has led to an ever-increasing level of the Go chess game system based on Monte Carlo search. Monte Carlo search has become a key technology for making decisions in the perfect information game scenario, and it has broad prospects in many real world applications.

MCM application area:
More and more extensive. It not only solves the difficult and complicated mathematical calculation problems such as multi-integral calculation, differential equation solving, integral equation solving, eigenvalue calculation and nonlinear equations solving, but also solves statistical physics, particle transport calculation, quantum thermodynamics. Computing, aerodynamics, nuclear physics, vacuum technology, systems science, information science, utilities, geology, financial engineering, macroeconomics, biomedicine, reliability, computer science, and machine learning in artificial intelligence Have been successfully applied.
MCM development process:
1) In the early 20th century, despite the thousands of experiments, the pi value obtained by the Monte Carlo method did not reach the accuracy of Zu Chongzhi in the 5th century AD. This may be the main reason why the traditional Monte Carlo method has not been popularized for a long time.
2) The development of computer technology has enabled the Monte Carlo method to gain rapid popularity in the last 10 years. With the modern Monte Carlo method, it is no longer necessary to experiment with one's own hands, but with the aid of the high-speed operation of the computer, the originally time-consuming and laborious experimental process becomes a quick and easy task. It is not only used to solve many complex scientific problems, but also often used by project managers.
MCM advantages:
1) The algorithm is simple, eliminating the complicated mathematical derivation and calculus process, so that the average person can understand and master;
2) Strong adaptability, the complexity of the geometry of the problem has little effect on it;
3) The speed is fast, the convergence of the method refers to the convergence in the sense of probability, so the increase of the dimension of the problem will not affect its convergence speed;
4) The storage is small, and the storage unit when dealing with a large-scale complex problem is very low.
MCM weaknesses:
If entering a random number in a pattern is not a random number as it is supposed to, but it constitutes a subtle non-random pattern, the Monte Carlo method can be used to solve the problem.
Comparison between MCM and GA:
Monte Carlo method MCM and genetic algorithm GA (please participate in the public number "Science and Technology Optimization Life" - artificial intelligence (28)) and other intelligent optimization algorithms are similar, are all random approximation methods, can not guarantee the optimal solution, etc. But they also have essential differences. 1) The level is not the same, MCM can only be called a method, GA is a bionic intelligence algorithm, much more complex than MCM. 2) Different fields of application, MCM is a kind of simulation statistics method. If the problem can be described as a form of statistic, then MCM can be used to solve it; while GA, etc. are suitable for large-scale combinatorial optimization problems and complex functions. For the best value, parameter optimization and so on.

Conclusion:
The Monte Carlo Method MCM, also called statistical simulation method, is a very important numerical method guided by probability statistics theory. Refers to the use of random numbers (or more commonly pseudo-random numbers) to solve many computational problems. The Monte Carlo method MCM solves practical problems by constructing random numbers that meet certain rules. It is widely used in financial engineering, macroeconomics, computational physics (such as particle transport calculations, quantum thermodynamics calculations, aerodynamic calculations) and machine learning in artificial intelligence.
Electronic Cable,Electronic Wire,Red Yellow Black Electron Wire,Connector Cable For Controller
Dongguan ZhiChuangXing Electronics Co., LTD , https://www.zcxelectronics.com