2017 has passed away. In the past year, human beings have once again become enthusiastic about technology, but the thoughts triggered by fanaticism point to a completely different direction.
An explosive breakthrough is that gravitational waves are experimentally confirmed, thus validating the predictions of Einstein's general theory of relativity. A few decades ago, Weber's gravitational wave experiments were already well-known, but the gravitational waves that he announced several times were not recognized in the world. Weber’s historical role has been lingering between the scientific martyrs and the rivers and lakes. The success of this gravitational wave detection undoubtedly defined Weber as a historical pioneer, which made his fateful fate the color of the tragic hero; at the same time, it also declared the great success of human rational thinking. The establishment of Einstein's general theory of relativity follows the classical theoretical research approach, from the establishment of the axiom system to the strict mathematical reasoning, to the precise physical prediction, and finally by the experimental test; the abstract Riemann geometry in mathematical reasoning transcends human intuition, and truly guides Einstein's establishment of a grand system is an aesthetic of the inherent harmony of the theoretical system.

Another disruptive development is artificial intelligence, especially the wave of machine learning. Over the past few years, the knowledge and skills of machine learning have been overwhelming. Students are being shocked by various academic advertisements every day. They are dazzled and difficult to adapt. They are all in the anxiety of being abandoned by the times. After several years of academic training, it is still impossible to carry out mathematical modeling and theoretical analysis of the problem, instead of "end-to-end" training skills. Whether such "alchemy" based on empirical statistics will eventually be elucidated and refined by strict theory. At present, benevolent sees benevolence, and wise sees wisdom. Wait for the foam to dissipate, and the time will distill the alcohol.

The third frenzy is interesting, bitcoin and blockchain. At the end of the year, the bitcoin market was becoming more and more fanatical, and it was increasingly out of the original heart of digital currency. Although human pursuit of money is increasingly irrational, the bitcoin network protocol designed by Nakamoto is based on the assumption of human reason. In the history of mankind, the financial trading system is based on trust. There is always a reliable central institution to certify the wealth value owned by individuals to certify the correctness of each transaction. Bitcoin has subverted these two points: the Bitcoin system does not require a trust institution as the center; the Bitcoin system is not traceable and cannot infer the owner from the account address. This digital currency system is based on two rational assumptions as follows: First, there are always more "good guys" on the bitcoin network than "bad guys". Second, the encryption algorithm based on elliptic curves is safe and cannot be easily cracked.

The rise of elliptic curve theory is due to the proof of Fermat's Last Theorem. Fermat guess equation When n is greater than 2, there is no integer solution. This speculation is like a cliff, and it has been on the historical road of the development of number theory for more than three hundred years. The most critical breakthrough comes from the elliptic curve. The Gushan-Shicun guess proposed by Gu Shanfeng established an important connection between the elliptic curve and the modular form (some periodic pure function). Although Gu Shanfeng had an insight into the secret, he could not prove that his newly married wife had committed suicide by dying. Later, Andrew. Andrew Wiles proved part of the Gushan-Shimura guess, thus proving the Fermat's theorem. The proof of Fermat's theorem is naturally a monument in the history of human thought. Gushan is a mathematics martyrdom, and it will eventually become a swan song. Wiles has been obsessed with dreams for decades. However, at that time, no one would expect Fermat's theorem to prove that the elliptic curve theory that was born would one day become the basis of the Bitcoin network.

The more difficult the theory is in mathematics, the more difficult it is to convert into an algorithm, so it is more and more secure. On a finite field, the algebraic cluster defined by the elliptic curve (the set of points of the solution) is a finite set of discrete points. Each elliptic curve and straight line has three intersection points, which we understand as the sum of three points is 0, thus defining a group structure on the algebraic cluster. In this group, we can construct problems that are easy to test but difficult to solve, so-called one-way functions, such as discrete logarithms. These one-way functions are used for digital signatures, making it easy for users to verify, but not forged, thus forming the basis of the Bitcoin protocol. Mathematically, the understanding of the elliptic curve group structure is crucial for the Bitcoin system.
Addition group of elliptic curvesElliptic curves have a form, and the necessary and sufficient conditions for a polynomial equation with distinct roots are non-zero. We look at the algebraic cluster here is the infinity point.

Figure 1. Addition on an elliptic curve
As shown in Figure 1, we consider defining an elliptic curve on the real number field. It intersects the line P and Q at the third point R. The R is the lead line, and the lead line and ellipse curve are placed in the fourth line. a little bit. The fourth point and R reciprocal, recorded as. Then we define the addition. After simple algebraic operations, we get the addition so defined that all points on the elliptic curve form an additive group, and the infinity point is a unit element. Figure 2. Multiplication on an elliptic curve.
Figure 2 shows the multiplication on the elliptic curve. If we pass the point G to do the tangent, the tangent intersects the elliptic curve at -2G and is reflected to get 2G. So, we can define 4G, 8G and so on.
The above geometric operations can be directly converted into algebraic operations. Let's make a straight line of two points, so here. Thus, we see that if the coefficients A and B of the elliptic curve are in a certain field K, the coordinates are also in the field K, and the coordinates of the sum are also in the field K. Thus, Poincare proved that the points E(K) of all coordinates in K on the elliptic curve E(R) on the real number domain (and the infinity points) constitute a subgroup.
Elliptic curve on the complex domain - Riemann surface
If the domain of the elliptic curve is a complex field, then the algebraic cluster of the elliptic curve constitutes a Riemannian face with a genus of one. First we define a grid point, then the tire is the quotient space.
Figure 4. Elliptic curve on the complex field.
We define the Willstras p-function, (Weierstrass p-funcTIon), then we make it. Here the Wilstrass p-function is a two-period function that satisfies periodic conditions.
At this time, the structure of the elliptic curve group is, that is, the topological tire. We fixed a positive integer N greater than 1, defining a subgroup, that is, a subgroup of points on the elliptic curve where all ranks can be divided by N. Then this subgroup is the product of two cyclic subgroups.
An elliptic curve on a rational number field If the domain of an elliptic curve is a rational number field, it has an infinite number of points. Mordell proved in 1922 that it is a finitely generated group. There is a finite point set, and any point can be expressed as
Further, here is the finite order flex subgroup of the elliptic curve, and r is called the rank of the elliptic curve. In 1977, Mazur proved that there are only 15 cases of the elliptic curve of the elbow group. However, the rank of the elliptic curve is still mysterious. It is speculated that for any large r, there is an elliptic curve on the rational number field whose rank is equal to r.
Elliptic curve over a finite field
Let p be a positive integer and be the integer domain of modulo p. An elliptic curve, satisfied, whose algebraic cluster is a discrete set of points, as shown in Figure 5, the same elliptic curve is on different finite fields, and its algebraic cluster contains a different number of discrete points.
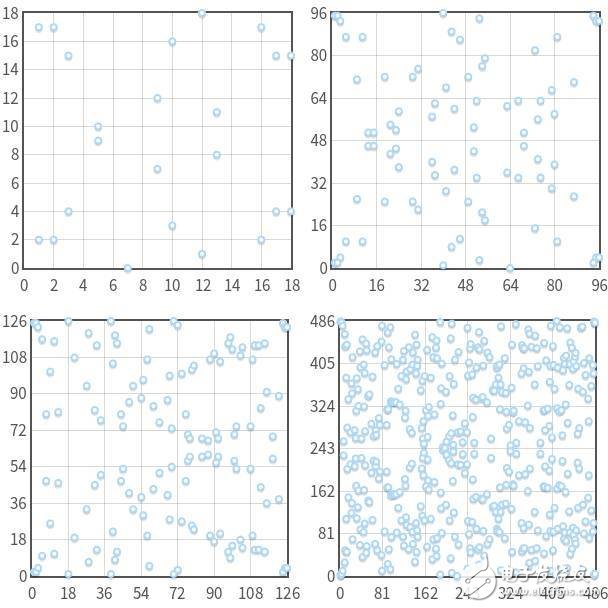
Figure 5. The same elliptic curve with different numbers of discrete points on different finite fields
In 1922, Hasse proved that the number of elliptic curve algebraic cluster points on the finite field and the difference of (p+1) are not more than twice the square root of p: In particular, if p is an exponent of 2, the so-called Koblitz curve, then.
Let the ellipse E be defined on a finite field, let S and T be two points on the elliptic curve, and find the integer m so that this problem is called the discrete logarithm problem. At present, the most effective method for solving discrete logarithms is the Pollard method, whose algorithm complexity is exponential complexity of k. The security of digital signatures in the Bitcoin protocol is the exponential complexity of the discrete logarithm problem.

In general, if the elliptic curve group has a richer structure, the difficulty of the discrete logarithm problem will be reduced. A common method in mathematics is to transform a finite field into another domain, especially a rational number domain, to establish a homomorphism between two elliptic curve groups, and in certain cases, the homomorphism can be enhanced to isomorphism. Specifically, the elliptic curve E(Q) on a rational number field is fixed, and its coefficient is p, we map it to the elliptic curve E(Fp) on the finite field, and the point P(x) on each E(Q) , y) is mapped to the point on E(Fp), assuming x=a/b, then. This mapping is called the ReducTIon Modulo p Map. If E(Fp) is not degenerate, then this mapping gives the homomorphism between the groups E(Q) and E(Fp). Crucially, if we choose a positive integer N, and p are mutually prime, then the ReduceTon Modulo p Map is isomorphic. The importance of this theorem cannot be overemphasized.
This method of transforming the basic number field of algebraic curves is very elegant. In essence, if we use finite fields, we get the number theory problem. If we use the complex field, we get the complex geometry problem of Riemannian surface. For example, the well-known elliptic curve L-sequence problem is the intersection of number theory and algebraic geometry. Let E be a fixed elliptic curve with coefficients A and B being integers. For any prime number p, we map E to the modulo p domain to get the elliptic curve E(Fp). We define the trace of E(Fp) as the famous L-series (L-series) to encode all traces to a function.
Wile proves that L(E, s) can be parsed and extended to the entire complex plane. s=1 is the zero of L(E,s). The famous Brich-Swinnerton-Dyer guess is the index of this zero, which is equal to the number of generators of the curve E(Q) on the rational domain. Recently, the Chinese mathematics star æ½ä¹‹çŽ® and Zhang Wei won the 2018 Mathematics “New Vision Awardâ€, which was donated by Google founder, founder of FaceBook, Russian rich Milner and Ma Huateng.
summaryThe elliptic curve is connected to algebraic geometry and number theory, and it contains the natural secrets. Its profoundness has made countless mathematicians fascinated and deeply loved. From the generosity of Gu Shanfeng, to the heroic epic of Wells, to the magical hand of Nakamoto, from the abstract theory of the altar of mathematics to the digital currency of financial markets, from the mathematicians’ decisive martyrdom to natural truth, to All the directions are arrogant and chaotic, and the opposite is true, but it is logical and seamless. The development of history is always beyond imagination, subverting everything, but it is also a cycle of heaven and earth. We are convinced that the pursuit of truth and the pursuit of money in human nature will remain unchanged: there will be more young talents, painstakingly searching for natural truths, and painstaking efforts; there will be more financial masters, flashing and moving, Turning the clouds and rain. With the further breakthrough of the elliptic curve theory, more financial innovations will be born again.

AC Input : 100V to 240V, DC Output: 12 volt at 2 amp rating . Please refer to the ASIN :B0746GCGQ8 if u need 10 units.
Type : Regulated Switching Power Supply with 2.1mm x 5.5mm plug , center positiveManufactured with high quality material and built-in protection of over current, over voltage, short circuits .
COMPACT DESIGN and LOW CONSUMPTION makes it ideal for taking around and using at home.
12v wall charger,12v switching adapter,(12V/2A) Switching Mode Power Adapter Wall Charger,12V 2A Power Supply Adapter,12 Volt 2 Amp Power Adapter,12V 3A Power Supply Adapter,12v3a wall charger
Shenzhen Waweis Technology Co., Ltd. , https://www.waweispowerasdapter.com