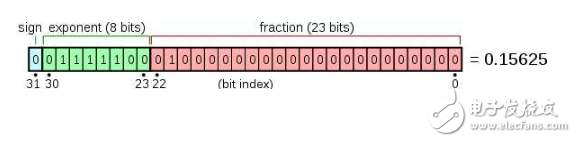
Single precision is such a format, 1 bit symbol, 8 bit index, 23 decimal places.
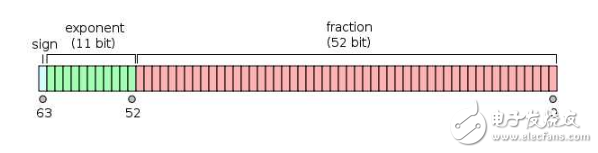
Double precision is a 1-bit symbol, 11-bit index, and 52-bit fraction.
The difference is that the range of values ​​it can store is different.
Double precision variables can store larger or smaller values ​​than single precision variables.
-- -- float can be assigned +/- 3.40282e+038
-- -- double can be assigned +/- 1.79769e+308
Meaning: It indicates that the range of single precision and double precision is different. Single precision, that is, float, generally takes 4 bytes in the computer, 32 bits, and the effective number is 7 bits; double precision is in the computer. The storage occupies 8 bytes, 64 bits, and the effective number of bits is 16 bits.
Reason: Regardless of whether the float or double storage on the computer follows the IEEE specification, using binary scientific notation, there are three parts: the sign bit, the exponent bit, and the mantissa part. The sign bit, exponent bit, and mantissa of the float are 1, 8, 23. The double precision is 1, 11, 52 respectively.
The accuracy mainly depends on the number of digits in the mantissa part. The float is 23 bits. Except for the case of all 0s, the minimum is 2 to the -23th power, which is approximately equal to 1.19 times 10 to the -7th power, so the fractional part of the float can only Accurate to the next 6 digits, plus one digit before the decimal point, that is, the significant digit is 7 digits. Similarly, the double mantissa part is 52 bits, and the smallest is 2 -52 powers, which is about 2.22 times 10 to the 16th power, so it is accurate to 15 decimal places, and the effective number of bits is 16 bits.
Single-precision and double-precision numeric types first appeared in C language (compared to common languages). In C language, single-precision types are called floating-point types (Float). As the name implies, data is stored by floating decimal points. These two data types were first developed for scientific calculations, and they provide scientific calculations with sufficient precision to store values ​​that require higher precision. But at the same time, he is also fully in line with the notion of numerical values ​​in scientific computing:
When we compare the lengths of two sticks, one method is to compare and discharge, one method is to measure the length separately. But in fact there are no two sticks of exactly the same length in the world. The accuracy of the length we measure is limited by the human visual ability and the accuracy of the measuring tools. In this sense, it doesn't make sense to judge whether the two sticks are the same length, because the result must be False, but we can compare which of them is longer or shorter. This example is a good summary of the original design and existence of single-precision/double-precision numeric types.
Based on the above understanding, the single-precision/double-precision numerical type is not an accurate numerical type from the beginning. It only guarantees that it is accurate within the accuracy of his numerical type, and the accuracy is not guaranteed. Say, a value of 5.1, it is likely that the actual value stored in the single-precision/double-precision value is 5.100000000001 or 5.09999999999999. The reasons for this phenomenon can be explained in two ways:
Simple explanation:You can try to set his width to 3.2CM in the properties panel of any control. When you finish typing, you will find that the value automatically becomes 3.199cm. No matter how you change it, you can't input 3.200CM. Because the actual value stored in the computer is not the value of CM, but the value of "缇" as the unit, and the ratio between "缇" and CM is a number that is difficult to be divided, so you enter After the completion, the computer automatically converts to the closest "缇" value, and then converts it to centimeters and displays it on the property panel. This multiplication and division, twice rounded off, the error comes out. Single-precision/double-precision is a similar principle. In the case of binary storage, single-precision/double-precision uses a similar method of similar scores, and such storage is impossible to be accurate.
Let's take a look at what the single-precision/double-precision values ​​we store into digital media. We use the following code to perform an anatomy of the single-precision type:
Public Declare Sub CopyMemory Lib “kernel32†Alias
"RtlMoveMemory" (DesTInaTIon As Any, Source As Any, ByVal Length As Long)
Public Sub floatTest() Dim dblVar As Single
dblVar = 5.731 / 8 dblOutput dblVar
dblVar = dblVar * 2 dblOutput dblVar
dblVar = dblVar * 2 dblOutput dblVar
dblVar = dblVar * 2 dblOutput dblVar
dblVar = dblVar * 2 dblOutput dblVar
dblVar = dblVar * 2 dblOutput dblVar
End Sub
Public Sub dblOutput(ByVal dblVar As Single) Dim bytVar(3) As Byte
Dim i As Integer, j As Integer Dim strVar As String
CopyMemory ByVal VarPtr(bytVar(0)), ByVal VarPtr(dblVar), 4 strVar = dblVar & “: †For i = 3 To 0 Step -1 For j = 7 To 0 Step -1
strVar = strVar & (bytVar(i) And 2 ^ j) / 2 ^ j
Next j
strVar = strVar & “ †Next i
Debug.Print strVar
End Sub
After running, we get the output (the output format is high left, low right):
.716375: 00111111 00110111 01100100 01011010 1.43275: 00111111 10110111 01100100 01011010 2.8655: 01000000 00110111 01100100 01011010 5.731: 01000000 10110111 01100100 01011010 11.462: 01000001 00110111 01100100 01011010 22.924: 01000001 10110111 01100100 01011010
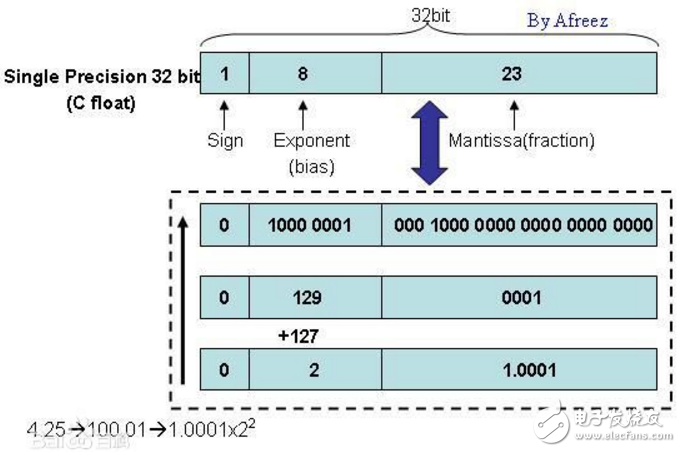
Here, we convert the single-precision type into a binary data output. Here we see that although the six numbers are completely different, their binary storage is strikingly similar. We see the red mark part, which is incremented by 1 each time. In fact, the single-precision data type uses the first bit from the upper bit as the positive and negative flag bit (green), and the second bit to the ninth bit, which is a cross-byte signed byte type data, which determines the decimal point movement. The direction and number of bits (red), the 10th to the 32nd bit holds an integer (blue). During the storage process, the computer first shifts the input value continuously (multiplication and division by 2) until the integer part of the number occupies all 24 The integer bit of the bit is then written to the floating point portion (red), and the shifted result is written to the integer portion (blue and green), and the fractional portion is discarded. When evaluating, it is the reverse process. It is first evaluated according to the positive and negative bits and the integer bits, and then shifted according to the integer of the red part (multiplied by the power of 2), and finally we get the single-precision value. The double precision value is the same principle, but the number of bits is more.
By dissecting the binary storage format of single-precision values, we can clearly see that in fact, single-precision/double-precision storage must pass multiplication and division, which must be rounded if your value is rounded in the division. Then, the initial value you assign is probably not exactly the same as the value you finally stored. The slight difference is not inconsistent with the single-precision/double-precision design goal.
When we use a single-precision/double-precision value in the database or in VBA code, you may not see the difference from the interface, but in the actual storage, this difference is really there, when you When comparing them equally, the system simply compares the binary, and the small differences that cannot be reflected on the interface are invisible in the face of binary comparison. Therefore, your comparison is equivalent to returning an unexpected False.
Why Lithium Battery?
Electricity is a must need in our daily life. Advanced technology has brought us various new ways for power supply. Battery, which can store energy and supply energy for our power needs, has been with us for years. Compared with traditional battery technology, lithium battery technology has drawn our attention. Nowadays, they are the common power source for our daily power supply demands. Your cell phones, laptops, electronic gear or even your vehicles, are powered with lithium batteries. With the massive and increasing demand for reliable power, lithium battery is an ideal power option.At UFO POWER, we are professional to offer rechargeable lithium batteries for your electronic equipment. Quality and reliability are the basic pillars of the success of our product. We have focused on lithium batteries pack manufacturing for more than 10 years.
Lithium batteries can be widely used for a variety of applications, including solar or wind energy storage, solar power system, telecom base station, camping, boat, fishing, recreational vehicles, golf carts and other applications. UFO lithium batteries are ready to be your reliable battery option.
Advantages of lithium batteries
Lithium batteries, as a new favorable battery option, have several outstanding advantages over their lead-acid counterparts:-- Deep depth of discharge. Lithium batteries are designed to last longer with a deep depth of discharge. It enables some electronics such as high-tech and smart devices to work for a longer time.
-- Fast charging speed. When using lithium batteries for your electronic device, you can save time for charging and improve working efficiency.
-- Long service life. The lithium batteries provides up to 2000 cycle life with proper use. The features of less maintenance and longevity makes it a perfect option for power supply.
-- Wide temperature range. The lithium batteries can withstand extreme temperature. It can work in a cold winter or hot environment without battery failure. It is suitable for outdoor applications.

Rechargeable Lithium Ion Battery,Lithium Polymer Battery,Lithium Car Battery,Lithium Iron Phosphate Battery
ShenZhen UFO Power Technology Co., Ltd. , https://www.ufobattery.com